A prime number is a natural number (greater than 1) that has exactly two factors, 1 and itself. In order to check if a number is prime or not, we can count the number of factors. If it is 2, then we say that the number is prime, else it is a composite number. Side note, non-prime numbers are called composite numbers.
Table of Contents
- How to check if a number is prime or not?
- Brute Force Python Implementation to check if a number is prime - O(N)
- O(sqrt(N)) method to check if a number is prime or not
- Sieve of Eratosthenes
How to check if a number is prime or not?
To check if a number is prime, we count its factors (or divisors). If the count is 2 then it is a prime number. So effectively, it seems like the problem of primality testing is as difficult as finding factors of a number. However, in case of prime numbers, we don’t really need to find all the factors, we just need the count.
The brute force method to check if n is prime would be to iterate from 1 to n and check if any number divides n. If the count is exactly 2 (1 and n itself) then n is a prime number.
Brute Force Python Implementation to check if a number is prime - O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def is_prime(n):
"""
Assumes that n is a positive natural number
"""
# We know 1 is not a prime number
if n == 1:
return False
# We store the number of factors in this variable
factors = 0
# This will loop from 1 to n
for i in xrange(1, n+1):
# Check if `i` divides `n`, if yes then we increment the factors
if n % i == 0:
factors += 1
# If total factors are exactly 2
if factors == 2:
return True
return False
# Test the above function
for x in xrange(1, 11):
print '%d: %s' % (x, is_prime(x))
# Output:
# 1: False
# 2: True
# 3: True
# 4: False
# 5: True
# 6: False
# 7: True
# 8: False
# 9: False
# 10: False
Time Complexity of the above approach is O(N), N is the number being tested for primality. So in case our number is of the order of 1000000000, then this method fails to return in feasible time. How can we optimize it? We can probably iterate from 1 to N/2, still the complexity is O(N).
O(sqrt(N)) method to check if a number is prime or not
While finding factors of a number we found that it is enough to iterate from 1 to sqrt(N) to find all the factors of N. So, from 1 to sqrt(N) we would find exactly 1 factor, i.e. 1 itself. Let’s iterate from 2 to sqrt(N). We won’t find any factor in this range. So, if we find any factor in this range, then we call that number a non-prime number, else it is a prime number.
Python Implementation - O(sqrt(N))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def is_prime(n):
"""
Assumes that n is a positive natural number
"""
# We know 1 is not a prime number
if n == 1:
return False
i = 2
# This will loop from 2 to int(sqrt(x))
while i*i <= n:
# Check if i divides x without leaving a remainder
if n % i == 0:
# This means that n has a factor in between 2 and sqrt(n)
# So it is not a prime number
return False
i += 1
# If we did not find any factor in the above loop,
# then n is a prime number
return True
for x in xrange(1, 11):
print '%d: %s' % (x, is_prime(x))
# Output:
# 1: False
# 2: True
# 3: True
# 4: False
# 5: True
# 6: False
# 7: True
# 8: False
# 9: False
# 10: False
print '%d: %s' % (1000000000, is_prime(1000000000))
# Output: 1000000000: False
print '%d: %s' % (1000000007, is_prime(1000000007))
# Output: 1000000007: True
C++ Implementation - O(sqrt(N))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
using namespace std;
bool is_prime(int n) {
// Assumes that n is a positive natural number
// We know 1 is not a prime number
if (n == 1) {
return false;
}
int i = 2;
// This will loop from 2 to int(sqrt(x))
while (i*i <= n) {
// Check if i divides x without leaving a remainder
if (n % i == 0) {
// This means that n has a factor in between 2 and sqrt(n)
// So it is not a prime number
return false;
}
i += 1;
}
// If we did not find any factor in the above loop,
// then n is a prime number
return true;
}
int main() {
for(int x=1; x<11; x++) {
cout << x << ": " << (is_prime(x) ? "true" : "false") << endl;
// Output:
// 1: false
// 2: true
// 3: true
// 4: false
// 5: true
// 6: false
// 7: true
// 8: false
// 9: false
// 10: false
}
cout << 1000000000 << ": " << (is_prime(1000000000) ? "true" : "false") << endl;
// Output: 1000000000: false
cout << 1000000007 << ": " << (is_prime(1000000007) ? "true" : "false") << endl;
// Output: 1000000007: true
return 0;
}
Time Complexity of the above algorithm is O(sqrt(N)). Go ahead, try to check for a number as large as 1000000000, this implementation will return the result in flash.
However, at times, we might need to find prime numbers in a given range. Let’s say the range is i to j. In this case, we loop from i to j and for each number we check if it is prime or not in O(sqrt(N)). So overall, we will end up with a solution with time complexity O((j-i) * sqrt(N)). Can we do any better?
Sieve of Eratosthenes
The idea behind Sieve of Eratosthenes is to cross out all the composites in the given range. Once we are sure that all composites are crossed out, we are left with all the primes in the given range. How do we cross out all the composites?
Let’s create a process to find all primes in the range 1 to N.
- Iterate from
2tosqrt(N), call iti - For each
i, we cross out all the multiples ofi, i.e.2*i,3*i.. and so on - If
iis already crossed out, we don’t do anything, because ifiis already crossed out, we are ensured that all multiples ofiare already crossed out in our previous iterations - In the end, we print out all the numbers that are not crossed out
Example: Let’s take a range [2, 25] and find all the primes in this list.
[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25]
- Iterate from
2tosqrt(25), call iti- So we iterate from
2to5
- So we iterate from
- For 2, cross all multiples of 2 i.e.
2*2,3*2,4*2.. and so on
[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25]
- For 3, cross all multiples of 3 i.e.
2*3,3*3,4*3.. and so on
[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25]
-
For 4, Ohh! 4 itself is already crossed out, so we are ensured that all its multiples are also crossed out
-
For 5, cross all multiples of 3 i.e.
2*5,3*5,4*5.. and so on
[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25]
Now, all the numbers that are not crossed out are prime numbers in the range [2, 25]. They are: [2, 3, 5, 7, 11, 13, 17, 19, 23]
A beautiful visualization of the above process was found on wikipedia2.
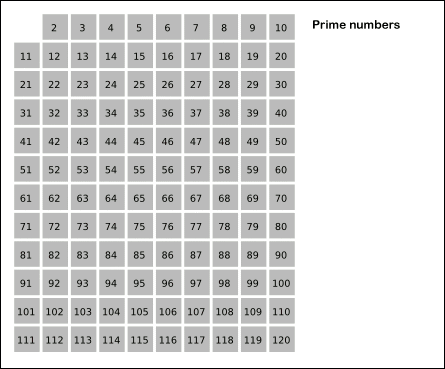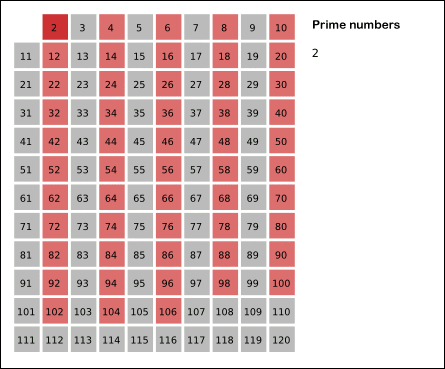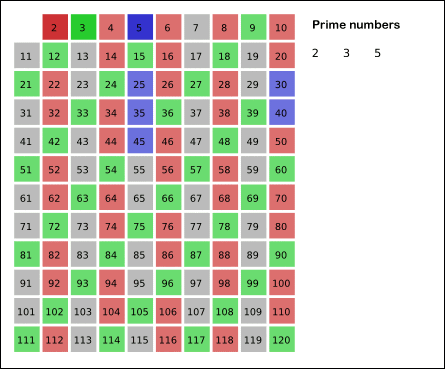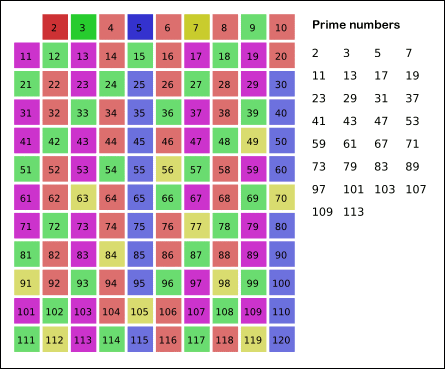
Let’s convert the above process into code.
Python implementation of Sieve of Eratosthenes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# We will find all primes in the range 1 to 120
# is_prime[i] = 1 means that i is prime and is_prime[i] = 0 means that i is composite
# Initially, we say all of them are prime
N = 121
is_prime = [1]*N
# We know 0 and 1 are composites
is_prime[0] = 0
is_prime[1] = 0
def sieve():
"""
We cross out all composites from 2 to sqrt(N)
"""
i = 2
# This will loop from 2 to int(sqrt(x))
while i*i <= N:
# If we already crossed out this number, then continue
if is_prime[i] == 0:
i += 1
continue
j = 2*i
while j < N:
# Cross out this as it is composite
is_prime[j] = 0
# j is incremented by i, because we want to cover all multiples of i
j += i
i += 1
sieve()
for i in xrange(1, N):
if is_prime[i] == 1:
print i,
# Output: 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113
C++ implementation of Sieve of Eratosthenes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
using namespace std;
// We will find all primes in the range 1 to 120
int const N = 121;
int is_prime[N];
bool sieve() {
// We cross out all composites from 2 to sqrt(N)
int i=2;
// This will loop from 2 to int(sqrt(x))
while(i*i <= N) {
// If we already crossed out this number, then continue
if(is_prime[i] == 0) {
i++;
continue;
}
int j = 2*i;
while(j < N) {
// Cross out this as it is composite
is_prime[j] = 0;
// j is incremented by i, because we want to cover all multiples of i
j += i;
}
i++;
}
}
int main() {
// is_prime[i] = 1 means that i is prime and is_prime[i] = 0 means that i is composite
// Initially, we say all of them are prime
for(int i=0; i<N; i++) {
is_prime[i] = 1;
}
// We know 0 and 1 are composites
is_prime[0] = 0;
is_prime[1] = 0;
sieve();
// Print all the primes in between 1 and 121
for(int i=1; i<N; i++) {
if(is_prime[i] == 1) {
cout << i << " ";
}
}
// Output: 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113
return 0;
}
Analysis of complexity:
- Space Complexity: We consume O(N) space for initializing
is_primearray. - Time Complexity: From the reference paper1, the first loop iterates from
2tosqrt(N), so it is at most O(sqrt(N)). And the time spent in removing the multiples is at most:
Hence, the overall upper bound for time complexity turns out to be O(N log log N). This is a bit confusing at first glance, however, with practice of analysis we will eventually feel comfortable with such proofs and BigO derivations.
References:
- [1]: http://research.cs.wisc.edu/techreports/1990/TR909.pdf
- [2]: https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
Got a burning question you might wanna get answered? Ask it in the comments.
